"Cреди всех картинок, которые может создавать компьютер, лишь немногие могут поспорить с фрактальными изображениями, когда идет речь о подлинной красоте. У большинства из нас слово "фрактал" вызывает в памяти цветные завитушки, формирующие сложный, тонкий и составной узор."

Джеф Проузис

Oпределение фрактала

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта "The Fractal Geometry of Nature". В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.









Одним из основных свойств фракталов является самоподобие. В самом простом случае, небольшая часть фрактала содержит информацию о всем фрактале.
Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому".









Роль фракталов в современном мире

Одно из главных применений фракталов - это машинная графика. С помощью них можно создать (описать) поверхности очень сложной формы, а изменяя всего несколько коэффициентов в уравнении, добиваться практически бесконечных вариантов исходного изображения. Фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.







Типы фракталов

- Геометрические фракталы
Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.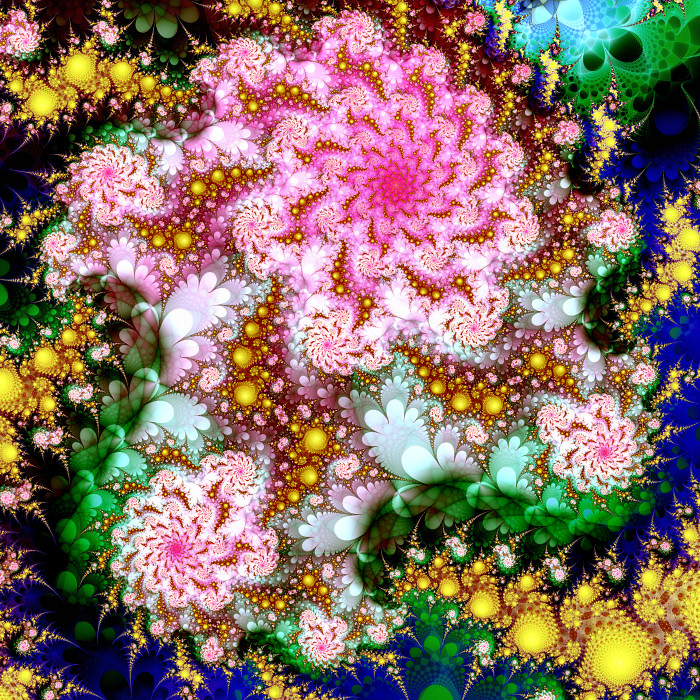











- Алгебраические фракталы
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоватся терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.









Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.







- Стохастические фракталы
Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.